Una puerta lógica, o compuerta lógica, es un dispositivo electrónico el cual es la expresión física de un operador booleano en la lógica de conmutación. Cada puerta lógica consiste en una red de dispositivos interruptores que cumple las condiciones booleanas para el operador particular. Son esencialmente circuitos de conmutación integrados en un chip.
Compuertas Lógicas directas:
Puerta SÍ o Buffer
La puerta lógica SÍ, realiza la función booleana igualdad. En la práctica se suele utilizar como amplificador de corriente o como seguidor de tensión, para adaptar impedancias (buffer en inglés).
La ecuación característica que describe el comportamiento de la puerta SÍ es:
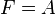
Su tabla de verdad es la siguiente:
| Entrada A | Salida A |
|---|---|
Puerta AND
La puerta lógica Y, más conocida por su nombre en inglés AND ( ), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
 ), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
La ecuación característica que describe el comportamiento de la puerta AND es:

Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida 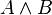 |
|---|---|---|
Así, desde el punto de vista de la aritmética módulo 2, la compuerta AND implementa el producto módulo 2.
Puerta OR
La puerta lógica O, más conocida por su nombre en inglés OR ( ), realiza la operación de suma lógica.
), realiza la operación de suma lógica.
 ), realiza la operación de suma lógica.
), realiza la operación de suma lógica.
La ecuación característica que describe el comportamiento de la puerta OR es:

Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida 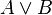 |
|---|---|---|
Podemos definir la puerta O como aquella que proporciona a su salida un 1 lógico si al menos una de sus entradas está a 1.
Puerta OR-exclusiva (XOR)
La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es el más (+) inscrito en un círculo. En la figura de la derecha pueden observarse sus símbolos en electrónica.
La ecuación característica que describe el comportamiento de la puerta XOR es:
 |-
|- 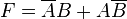
Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida  |
|---|---|---|
Se puede definir esta puerta como aquella que da por resultado uno, cuando los valores en las entradas son distintos. ej: 1 y 0, 0 y 1 (en una compuerta de dos entradas). Se obtiene cuando ambas entradas tienen distinto valor.
Si la puerta tuviese tres o más entradas , la XOR tomaría la función de suma de paridad, cuenta el número de unos a la entrada y si son un número impar, pone un 1 a la salida, para que el número de unos pase a ser par. Esto es así porque la operación XOR es asociativa, para tres entradas escribiríamos: a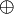 (b
(b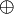 c) o bien (a
c) o bien (a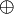 b)
b)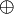 c. Su tabla de verdad sería:
c. Su tabla de verdad sería:
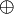 (b
(b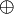 c) o bien (a
c) o bien (a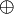 b)
b)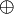 c. Su tabla de verdad sería:
c. Su tabla de verdad sería:| Entrada A | Entrada B | Entrada C | Salida 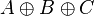 |
|---|---|---|---|
Desde el punto de vista de la aritmética módulo 2, la puerta XOR implementa la suma módulo 2, pero mucho más simple de ver, la salida tendrá un 1 siempre que el número de entradas a 1 sea impar.
Compuertas Lógicas negadas:
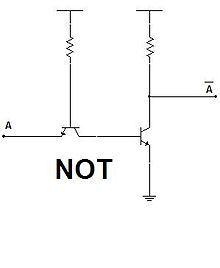
Puerta NO (NOT)
La puerta lógica NO (NOT en inglés) realiza la función booleana de inversión o negación de una variable lógica. Una variable lógica A a la cual se le aplica la negación se pronuncia como "no A" o "A negada".
La ecuación característica que describe el comportamiento de la puerta NOT es:

Su tabla de verdad es la siguiente:
| Entrada A | Salida 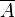 |
|---|---|
Se puede definir como una puerta que proporciona el estado inverso del que esté en su entrada.
Puerta NO-Y (NAND)
La puerta lógica NO-Y, más conocida por su nombre en inglés NAND, realiza la operación de producto lógico negado. En la figura de la derecha pueden observarse sus símbolos en electrónica.
La ecuación característica que describe el comportamiento de la puerta NAND es:

Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida  |
|---|---|---|
Podemos definir la puerta NO-Y como aquella que proporciona a su salida un 0 lógico únicamente cuando todas sus entradas están a 1.
Puerta NO-O (NOR)
La puerta lógica NO-O, más conocida por su nombre en inglés NOR, realiza la operación de suma lógica negada. En la figura de la derecha pueden observarse sus símbolos en electrónica.
La ecuación característica que describe el comportamiento de la puerta NOR es:

Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida  |
|---|---|---|
Podemos definir la puerta NO-O como aquella que proporciona a su salida un 1 lógico sólo cuando todas sus entradas están a 0. La puerta lógica NOR constituye un conjunto completo de operadores.
Puerta equivalencia (XNOR)
La puerta lógica equivalencia, realiza la función booleana AB+~A~B. Su símbolo es un punto (·) inscrito en un círculo. En la figura de la derecha pueden observarse sus símbolos en electrónica. La ecuación característica que describe el comportamiento de la puerta XNOR es:

Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida  |
|---|---|---|
Se puede definir esta puerta como aquella que proporciona un 1 lógico, sólo si las dos entradas son iguales, esto es, 0 y 0 ó 1 y 1 (2 encendidos o 2 apagados). Sólo es verdadero si ambos componentes tiene el mismo valor lógico.
PRACTICA 1 COMPUERTA LOGICA OR
Material:
Protovolt
1 Compuerta 7432
1 Compuerta 7408
1 Compuerta 7504
4 Diodos Led
1 Dip switch
1 Circuito Integrado 7805
1 Capacitor
1 metro de Cable
La finalidad de esta practica es que con el dip switch, prendan los 8 diodos led, utilizando la compuerta or.
PRACTICA 2 COMPUESRTAS LOGICAS AND,OR, NOT
Material:
Protovolt
1 Compuerta 7432
1 Compuerta 7408
1 Compuerta 7404
4 Diodos Led
1 Dip switch
1 Capacitor
1 metro de Cable
Resistencias
Conclusiones:
En las dos practicas se utilizaron las compuertas AND, OR y NOT con la finalidad de encender los diodos por medio de un dip switch, este indica cual debe de encender y apagar, utilizando los siguientes circuitos uno de las más utilizadas es la TTL (Transistor Transistor Logic). El circuito 7432 en sus distintas versiones (L, LS, S...), integra cuatro puertas suma (OR) de dos entradas en un encapsulado de 14 patillas, dos de las cuales son la de alimentación +5V(14) y masa (7).
Por otra parte el circuito 7408 integra también cuatro puertas, pero ahora multiplicación (AND) y sus terminales de alimentación.








Excelente información sobre las Compuertas lógicas, es algo que precisamente andaba buscanndo.
ResponderEliminar